Homework 3

Posted by Java Course Staff on October 23, 2016

第三次作业

截止时间: 2016年11月20日 09:00

这次作业的内容是用 shazam算法 实现音频检索(听歌识曲)。 shazam算法一共可以分成4个模块: 音频文件读取、指纹提取(hashing)、指纹存取、和指纹匹配。 关于这四个模块到底做什么，以及它们之间的关系，已经在群文件 ppt 中详细说明。

建议大家组队完成项目，一队3-4人为宜，最多4人。分工自行协商，每个人至少负责一个完整的模块。

知识性的内容已经在ppt中做了充分的介绍。在网页中主要是介绍提交的注意事项。

团队要求

  1. 只需队长建库，其他人不需建库。队长需在根目录下放一个成员名单，说明成员（含队长）的姓名、学号和分工。
  2. 每个人至少2次commit，否则此人不给分。
  3. 远程仓库的目录结构要和本地intellij/eclipse项目的目录结构一致。 不得在项目外再套文件夹。 换句话说，git根目录就是项目根目录。
  4. 所有文档(截图，txt等)放在项目根目录的doc文件夹下。
  5. 由于音频文件过大，不得放在项目目录中。请自行在程序入口放置Scanner来读取音频文件(夹)的路径。
  6. 一个模块一个package。
  7. 有merge commit的团队，可以加团队分。

两个建议:

  1. 多人合作的项目总要有一个初始版本，这样才方便其他人在这个版本上一点一点地推进项目。 音频文件读取是最固定的模块，因此适合作为初始版本。
  2. 每次打开项目之前一定别忘了先pull一下！！！

音频读取

  1. 音频文件一律采用【PCM WAV格式存储，位深度16bit，采样率44100Hz，单声道，不携带元信息。】
  2. 样例音频库 提取码 4zk2
  3. 写一个测试类: 任挑一首歌或其片段，把它的时序信息输出到txt。 之后把txt中内容粘贴到matlab，同时用matlab读取原始音频，比较两个波形。

指纹提取

这个模块没有有效的单元测试手段，只能看最终结果。

加分项：用O(n)复杂度实现”在4096个频率中找到能量最大的m个频率”。这是腾讯面试题，希望大家引起重视。 参考书：《算法导论》第三版，9.3节。 参考博文：http://blog.csdn.net/v_JULY_v/article/details/6370650

匹配打分

匹配至少5个歌曲片段，结果截图。

指纹存取(即数据库模块)

  1. 允许的数据库: MySQL，PostgreSQL。严禁使用Oracle，因为它会给队友带来很多麻烦。
  2. 在lib中附加jdbc引擎，并提交到git。
  3. 写一个测试类: 查询并输出当前时间。
  4. 保留建表SQL。

提交内容小结

  1. 项目代码。
  2. 建表sql，放在doc目录下。
  3. 波形对比截图。
  4. 查询当前时间截图。
  5. 至少5个匹配结果截图。

需要的工具小结

除编程工具(jdk、intellij/eclipse、数据库)外，可能还需要UltraEdit、Adobe Audition、Matlab。

附录

如何生成PCM WAV文件？

以Adobe Audition为例，

批量转换:

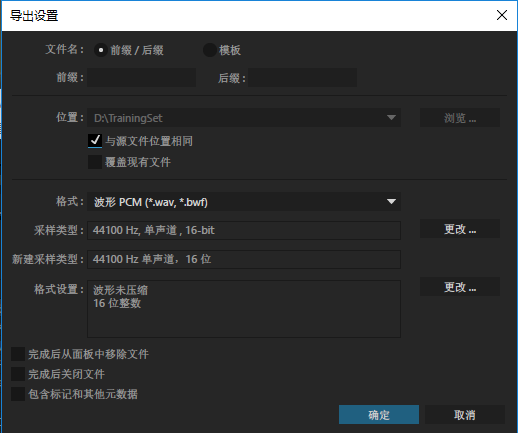
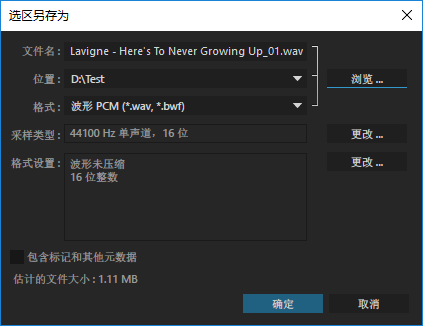
BatchConvert

保存选区:

BatchConvert

如何在matlab中验证音频解析的结果？

建议自己截一段几秒十几秒的音乐来验证，不要用整首歌，太大了。

** 2016-11-04 更新 **

首先，把算出来的double数组打印到csv文件。

PrintWriter out = new PrintWriter(new FileWriter(new File("test.csv")));
for (int i=0; i < sequence.length; ++i) {
	out.printf("%.2f,\n", sequence[i]);
}

打出来的内容就是Matlab中的一个数组变量. 之后在Matlab中输入

a = csvread('test.csv');
a = a(:,1);

之后在Matlab中直接读取原音频，生成变量b。

[b sr] = audioread('音频目录');

b是时序数据，sr是采样率。

最后用Matlab绘制a和b的波形图。

subplot(2,1,1), plot(a./32768); subplot(2,1,2), plot(b);

会出现这样的一个图表：

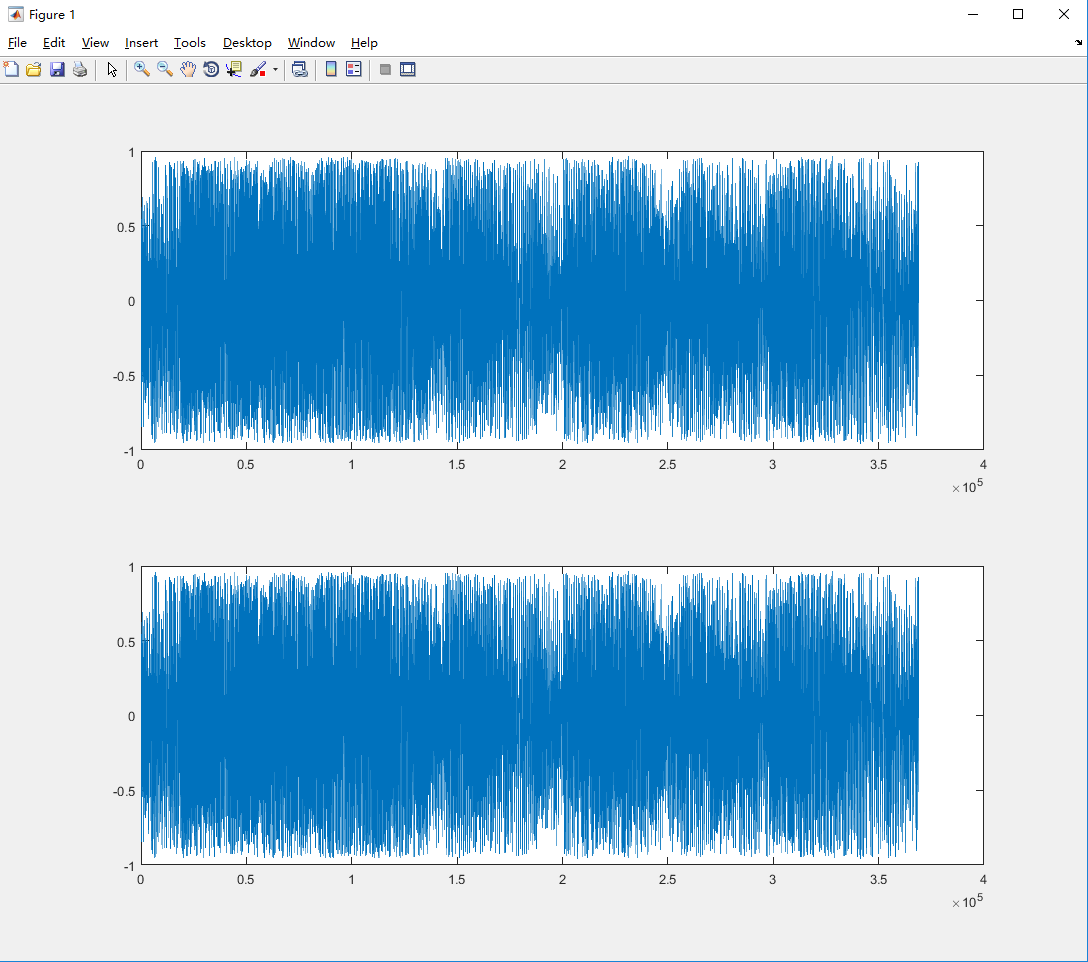
Matlab

上面是你自己算出来的，下面是Matlab读出来的。如果你的和Matlab的波形是一样的，就说明文件读取成功了。

傅里叶代码(2016-11-04)

表扬提早入手的同学，也恳请大家原谅我的疏忽：没有检查网上代码的正确性而给大家带来不便。

这次的代码是完全忠于算法导论实现的。有兴趣的可以参照算法导论的中英讲解。

复数类

public class Complex {
    private double a, b;
    public Complex(double _a, double _b) {
        a = _a;
        b = _b;
    }
    public Complex() {
        a = 0;
        b = 0;
    }

    public Complex add(final Complex e) {
        return new Complex(a + e.a, b + e.b);
    }

    public Complex sub(final Complex e) {
        return new Complex(a - e.a, b - e.b);
    }

    public Complex mul(final Complex e) {
        return new Complex (a * e.a - b * e.b, a * e.b + b * e.a);
    }

    public double abs() {
        // use hypot instead of sqrt(pow(a, 2), pow(b, 2))
        // to improve performance
        return Math.hypot(a, b);
    }
}

Bit Reverse函数

做【基-2】傅里叶变换之前，要先按照（无符号）逆比特序交换下标。具体原因请查阅算法导论。

这里简单说一下什么是逆比特序：就是把下标为无符号整数a和b的两个数组元素交换位置，其中b的比特是a的倒序比特。

private static void bit_reverse(Complex[] y) {
    int i, j, k;
    for (i = 1, j = y.length / 2; i < y.length - 1; ++i) {
        if (i < j) {
            Complex temp = y[i];
            y[i] = y[j];
            y[j] = temp;
        }
        k = y.length / 2;
        while (j >= k) {
            j -= k;            // eliminate leading 1.
            k /= 2;
            if (k == 0)        // cutting branches.
                break;
        }
        if (j < k)             // add leading 1.
            j += k;
    }
}

FFT主体函数

关键词：旋转因子、蝴蝶变换

private static Complex[] fft(Complex[] y){
    bit_reverse(y);
    int j, k, h;
    for (h = 2; h <= y.length; h <<= 1) {
        // twiddle factor 旋转因子
        Complex omega_n = new Complex(Math.cos(-2 * Math.PI / h), Math.sin(-2 * Math.PI / h));
        for (j = 0; j < y.length; j += h) {
            Complex omega = new Complex(1, 0);
            // butterfly transformation
            for (k = j; k < j + h / 2; ++k) {
                Complex  u = y[k];
                Complex  t = omega.mul(y[k + h / 2]);
                      y[k] = u.add(t);
                y[k + h/2] = u.sub(t);
                     omega = omega.mul(omega_n);
            }
        }
    }
    return y;
}

FFT最后一步

每个复数的模（绝对值）和振幅是正相关的

public static final WINDOW_SIZE = 4096;

public static double[] fft(double[] slice) {
    if (slice.length != WINDOW_SIZE)
        throw new RuntimeException("FFT::fft(double[] slice) - " +
                "The window size is not equal to the required window size (" + WINDOW_SIZE + ")");

    Complex[] x = new Complex[WINDOW_SIZE];

    /**
     * Convert the time-domain series as Complex series whose imaginary parts are zeros.
     */
    for (int i = 0; i < WINDOW_SIZE; ++i) {
        x[i] = new Complex(slice[i], 0);
    }

    Complex[] res = fft(x);

    double[] ret = new double[WINDOW_SIZE];
    for (int i = 0; i < WINDOW_SIZE; ++i) {
        /**
         * The magnitude of each frequency.
         */
        ret[i] = res[i].abs();
    }
    return ret;
}

指纹提取的部分实现

代码中append函数内部有一个TODO，这一块是找出每一帧音频中能量较高的N个频率，要自己实现。

** 2016-11-04 补充说明 **

既可以使用N最值法，也可以使用分块最值法。采用N最值法的如果用O(n)复杂度算法，有分数奖励。

public class Fingerprint {

	// DO NOT write FFT.WINDOW_SIZE / 44100, it equals to 0 forever!!
    public static final double scaling = FFT.WINDOW_SIZE / 44100.0;

    public static final int N = 3;

    private ArrayList<int[]> constel_data = new ArrayList<>();
    private int id;

    /**
     * For songs about to add into DB
     * @param id
     */
    public Fingerprint(int id) {
        this.id = id;
    }

    /**
     * For songs about to be searched
     */
    public Fingerprint() {
        this.id = -1;
    }

    /**
     * Append a column of frequency peaks to the constellation map.
     * A frequency peak is a frequency value whose amplitude is the highest among
     * all frequencies in a frequency interval.
     *
     * @param freqDomain The frequency domain generated by FFT.
     */
    public void append(double[] freqDomain) {
        int[] freqPeaks = new int[N];

        /**
         * TODO: Either find N frequencies with the highest amplitude(energy),
         * or find the frequency with the max energy within each interval.
         */

        constel_data.add(freqPeaks);
    }

    /**
     * Generate fingerprints using Combinational Hash.
     * For each frequency peak, generate 6 fingerprints with its 6 successors.
     *
     * @return
     */
    public ArrayList<ShazamHash> combineHash() {
        if (constel_data.size() < 3)
            throw new RuntimeException("Too few frequency peaks");
        ArrayList<ShazamHash> hashes = new ArrayList<>();
        for (int i = 0; i < constel_data.size() - 2; ++i) {
            for (int k = 0; k < interval_num; ++k) {

            	// "Combine" with all peak frequencies inside its next two frames.
                for (int j = 1; j <= 2; ++j) {
                    for (int kk = 1; kk < interval_num; ++kk) {
                        ShazamHash hash = new ShazamHash();
                        hash.f1 = (short) constel_data.get(i)[k];
                        hash.f2 = (short) constel_data.get(i + j)[kk];
                        hash.dt = (short) j;
                        hash.offset = i;
                        hash.id = id;
                        hashes.add(hash);
                    }
                }
            }
        }
        return hashes;
    }
}
CATALOG
    FRIENDS